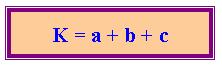Segitiga merupakan bangun datar yang unik. Karena setiap segi-n yang
lain merupakan gabungan dari beberapa segitiga. Misalnya saja persegi.
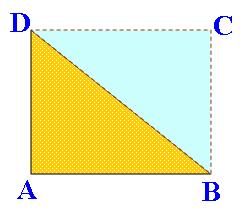
Persegi, minimal dapat dibentuk dengan dua segitiga siku-siku.
Segitiga merupakan bangun datar yang unik. Karena setiap segi-n yang
lain merupakan gabungan dari beberapa segitiga. Misalnya saja persegi.
Persegi, minimal dapat dibentuk dengan dua segitiga siku-siku.Begitu pula segi-5, segi-6, trapezium, laying-layang, dan sebagainya. Segitiga adalah bangun datar yang mempunyai sisi sebanyak tiga buah. Jumlah sudut di dalam segitiga adalah 180 derajat.
Segitiga terdiri dari tiga sisi. Yang paling terkenal di dalam segitiga dan menjadi konsep utamanya yaitu jumlah dua sisi segitiga pasti lebih besar dari pada sisi yang lain. Misalnya segitiga dengan panjang sisi-sisinya yaitu 3, 4 dan 5.
Inilah yang disebut sebagai ketaksamaan segitiga.
Dari sini kita bisa menebak apakah ada segitiga yang mempunyai panjang sisi 6, 2 dan 3. Tentunya tidak ada. Karena
Jenis-jenis segitiga berdasarkan besar sudut yang dibentuknya.
Segitiga siku-siku.
Segitiga siku-siku ini adalah segitiga yang salah satu sudutnya adalah 90 derajat. Teorema terkenal di dalam segitiga siku-siku adalah teorema Pythagoras. Segitiga siku-siku adalah segitiga yang unik. Segitiga ini juga digunakan di dalam perbandingan trigonometri.
Segitiga lancip
Adalah segitiga yang ketiga sudutnya merupakan sudut lancip
Segitiga tumpul
Segitiga yang salah satu sudutnya adalah sudut tumpul
Berdasarkan panjang sisinya, segitiga dibedakan menjadi
Segitiga sama sisi
Adalah segitiga yang ketiga sisinya mempunyai panjang yang sama. Segitiga ini juga tentunya mempunyai sudut yang sama. Yaitu 60 derajat. Ingat bahwa di dalam segitiga, jumlah sudut-sudut di dalam segitiga adalah 180 derajat. Segitiga sama sisi ini merupakan segitiga yang unik. Garis tinggi pada segitiga ini semuanya mempunyai panjang yang sama. Selain itu, kita juga dapat mencari rumus umum luas segitiga sama sisi tanpa mencari garis tingginya terlebih dahulu.
Segitiga sama kaki
Segitiga sama kaki adalah segitiga yang mempunyai dua sisi yang sama panjang. segitiga sama kaki pasti mempunyai dua sudut yang besarnya sama. Segitiga sama sisi juga bisa dikatakan segitiga sama kaki. Tetapi segitiga sama kaki tidak bisa dikatakan sebagai segitiga sama sisi. Segitiga sama kaki
Segitiga sebarang
Segitiga sebarang adalah segitiga yang panjang sisinya tidak ada yang sama antara yang satu dengan yang lainnya. Segitiga sebarang ini adalah segitiga yang mudah dibuat. Yang terpenting adalah memenuhi syarat bahwa dua sisi apabila dijumlahkan hasilnya pasti lebih besar dari pada sisi-sisi yang lainnya.
Dari jenis-jenis segitiga yang telah disebutkan di atas. Dapat kita kombinasikan menjadi segitiga-segitiga yang unik. Antara lain
Segitiga lancip sebarang
Ini adalah segitiga yang ketiga sudutnya lancip dan ketiga sisinya tidak ada yang sama panjang.
Segitiga lancip sama kaki
Sesuai namanya, segitiga ini mempunyai sudut-sudut yang semuanya merupakan sudut lancip dan ada dua sisi yang mempunyai panjang yang sama.
Segitiga siku-siku sebarang
Salah satu sudutnya adalah 90 derajat dan panjang sisinya tidak ada yang sama. Ini biasanya terdapat pada segitiga tripel Pythagoras. Yaitu segitiga siku-siku yang tidak mempunyai panjang sisi yang sama.
Segitiga siku-siku sama kaki
Ini adalah segitiga unik. Merupakan segitiga siku-siku yaitu salah satu sudutnya yaitu 90 derajat. Dan mempunyai dua sisi dengan panjang yang sama. Tentunya kedua sisi yang mempunyai panjang yang sama adalah sisi yang ada pada samping sudut 90 derajat. Kalau pada segitiga siku-siku ada yang namanya sisi miring. Yaitu sisi yang letaknya di depan sudut 90 derajat. Segitiga siku-siku sama kaki ini juga mempunyai dua sudut yang sama. Ini akibat dari kata-kata sama kaki.
Segitiga tumpul sebarang
Segitiga yang salah satu sudutnya adalah merupakan sudut tumpul dan panjang sisinya tidak ada yang sama
Segitiga tumpul sama kaki
Adalah segitiga yang salah satu sudutnya merupakan sudut tumpul dan ada dua sisi yang mempunyai panjang sama. Segitiga tumpul sama kaki ini juga merupakan segitiga yang cukup unik dari segi bentuk. Sudut yang lainnya dari segitiga ini adalah besarnya sama. Dan pasti merupakan sudut lancip.
keliling dan luas segitiga
Garis Tinggi Segitiga
Garis tinggi adalah garis yang ditarik dari salah satu titik sudut dan tegak lurus dengan sisi di depannya.
Karena segitiga memiliki tiga buah titik sudut, maka setiap segitiga memiliki tiga buah garis tinggi.
Alas Segitiga
Setiap sisi segitiga dapat dipandang sebagai alas sebuah segitiga.
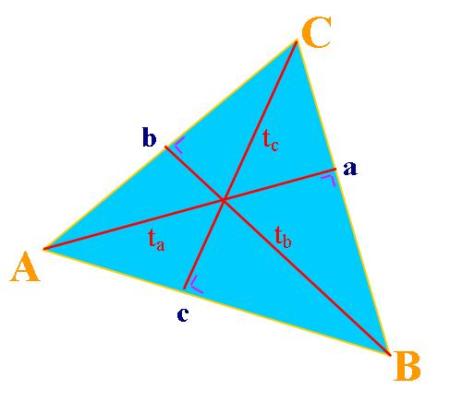
Perhatikan gambar berikut :
Sisi  AB disebut juga sebagai sisi c, karena letaknya di depan sudut C. Demikian juga sisi
AB disebut juga sebagai sisi c, karena letaknya di depan sudut C. Demikian juga sisi  BC dan
BC dan  AC disebut juga sebagai sisi a dan sisi b
AC disebut juga sebagai sisi a dan sisi b
 AB disebut juga sebagai sisi c, karena letaknya di depan sudut C. Demikian juga sisi
AB disebut juga sebagai sisi c, karena letaknya di depan sudut C. Demikian juga sisi  BC dan
BC dan  AC disebut juga sebagai sisi a dan sisi b
AC disebut juga sebagai sisi a dan sisi b
Garis tinggi yang dibuat dari titik sudut C disebut tc, karena tegak lurus dengan alas atau sisi c atau  AB. Demikian pula dengan garis tinggi yang dibuat dati titik sudut B dan A disebut tb dan ta.
AB. Demikian pula dengan garis tinggi yang dibuat dati titik sudut B dan A disebut tb dan ta.
 AB. Demikian pula dengan garis tinggi yang dibuat dati titik sudut B dan A disebut tb dan ta.
AB. Demikian pula dengan garis tinggi yang dibuat dati titik sudut B dan A disebut tb dan ta.
Keliling Segitiga
Keliling sebuah bidang datar adalah jumlah panjang
sisi-sisi yang membatasi bidang datar tersebut. Jadi, keliling segitiga
adalah jumlah panjang ketiga sisinya.
Jika K menyatakan keliling segitiga ABC maka
K = AB + BC + AC
K = c + a + b
Jadi keliling segitiga dirumuskan sebagai berikut:
Luas Segitiga
Luas segitiga adalah setengah hasil kali panjang alas dan tingginya
Keterangan :
a = alas
b = tinggi
 Title : Rangkuman tentang segitiga
Title : Rangkuman tentang segitiga Posted by :
Published : 2013-03-16T04:11:00-07:00